Estadística
jueves, 25 de junio de 2015
miércoles, 24 de junio de 2015
Estadística y su Historia
La
palabra Estadística procede del vocablo ¨ Estado¨, pues era función
principal de los Gobiernos de los Estados establecer registros de población, nacimientos, defunciones, impuestos,
cosechas. La necesidad de poseer datos
cifrados sobre la población y sus condiciones materiales de existencia han
debido hacerse sentir desde que se establecieron sociedades humanas organizadas. Desde
los comienzos de la civilización han
existido formas sencillas de estadística, pues ya se utilizaban representaciones gráficas y otros símbolos en pieles, rocas, palos
de madera y paredes de cuevas para contar
el número de personas, animales o ciertas cosas. Hacia el año
3000 a.C. los babilonios usaban ya pequeñas
tablillas de arcilla para recopilar
datos en tablas sobre la producción agrícola y de los géneros vendidos o
cambiados mediante trueque.
Definición de estadística
La estadística es una rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones.
Conceptos básicos
En estadística existen una serie de conceptos fundamentales para una mejor comprensión, entre los principales tenemos: Unidades elementales, datos, población, muestra, muestreo, variable, modalidad, moda.
Unidades
elementales
Son las personas, animales o cosas de las
cuales se desea saber algo. Por ejemplo
los alumnos del colegio, las vacas de una granja, el número de hijos hombres
por familia del barrio x.
El concepto de población en estadística va más allá de lo que comúnmente se conoce
como tal. Una población se precisa
como un conjunto finito o infinito de personas,
animales o cosas que presentan
características comunes. Por ejemplo
los estudiantes del grado sexto, el conjunto de profesores del colegio.
Se llama muestra a una parte de la población
a estudiar, en otras palabras es un subconjunto
de la población. Por ejemplo:
Población Los alumnos del grado sexto.
Muestra Los alumnos de sexto A
Unidades elementales Los alumnos
Es el método a utilizar para recolectar
información de las unidades elementales.
Entre los principales métodos tenemos las encuestas,
test, cuestionarios, entrevistas.
Son las observaciones que se hacen de las
personas, animales o cosas. Por ejemplo:
La mayoría de los alumnos de
sexto A son hombres.
Son
las características o cualidades de las personas, animales o cosas. Por ejemplo: La edad, estatura, peso,
color de ojos, tipo de religión, estado civil, entre otras.
Las variables estadísticas se
clasifican en dos, cualitativas y cuantitativas.
· Las variables
cualitativas son aquellas que se refieren a características o cualidades
de las personas, animales o cosas, que no pueden ser medidas con números. Por ejemplo:
El estado civil, sexo, color de ojos, preferencias políticas, entre otras. Se puede
distinguir dos tipos de variable
cualitativa:
Variable cualitativa nominal: Es aquella que presenta modalidades no numéricas, que no
admiten un criterio de orden. Por
ejemplo: El estado civil, con
las siguientes modalidades: soltero,
casado, separado, divorciado y viudo.
Variable cualitativa ordinal o
variable cuasi cuantitativa: Es aquella que
presenta modalidades no numéricas, en las que existe un orden. Por ejemplo: La nota en un examen, con sus modalidades: Superior, básico, aceptable, bajo.
Puesto conseguido en una prueba deportiva: 1º, 2º,
3º, ………
Medallas
de una prueba deportiva: Oro,
plata, bronce.
· Las
variables cuantitativas: Son aquellas que se expresan mediante un número, por tanto se
pueden realizar operaciones aritméticas con ella. Por ejemplo: La Edad, estatura, peso, número de hijos, número de hermanos. Se pueden
distinguir dos tipos de variables cuantitativas:
Variable discreta:
Es aquella que toma valores aislados, es decir enteros, por
lo tanto no admite valores intermedios entre dos valores
específicos. Por ejemplo: El número
de hermanos de 5 amigos: 2, 1, 0, 1, 3.
Variable continua: Es
aquella que
puede tomar valores comprendidos entre dos
números. Por ejemplo:
La altura de los 5 amigos: 1.73, 1.82, 1.77, 1.69, 1.75.
Modalidad de una variable
La modalidad de una variable, solo es
aplicable a variables cualitativas, y se puede decir que son las posibilidades
que puede tomar dicha variable. Por ejemplo:
La variable, partido político tiene
las siguientes modalidades:
Modalidad
Liberal
Conservador
Uribista
Alianza democrática
Partido verde
La variable Tipo de religión
Modalidad
Católico
Protestante
Evangélico
Budista
Ortodoxo
La variable Estado civil
Modalidad
Casado(a)
Soltero(a)
Separado(a)
Unión libre
Viudo(a)
La
estadística se clasifica en dos tipos, descriptiva
e inductiva.
Es
aquella que tiene por objeto fundamental
describir y analizar las características de un conjunto de datos, obteniéndose de esa manera conclusiones sobre las características de dicho conjunto y sobre
las relaciones existentes con otras poblaciones, a fin de compararlas.
Está fundamentada en los
resultados obtenidos del análisis de una muestra
de población, con el fin de inducir o inferir el comportamiento o
característica de la población, por lo que recibe también el nombre de Inferencia estadística. Se puede decir
que son procedimientos estadísticos que
sirven para deducir o inferir algo acerca
de un conjunto de datos numéricos
(población), seleccionando un grupo
menor de ellos (muestra).
Medidas de tendencia central
La NOTA promedio de matemáticas, en el grupo de 10 estudiantes es de 3.
lunes, 22 de junio de 2015
Tablas estadísticas
Las tablas estadísticas se utilizan para representar
todos los DATOS que se recogen de
una población determinada. En una tabla estadística encontraremos las siguientes partes:
Para entender mucho mejor el concepto de las tablas estadísticas, veamos el siguiente ejemplo.
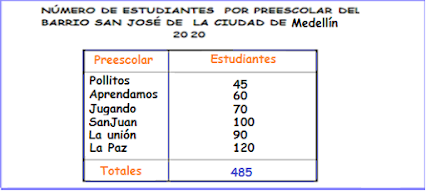
Se hizo una encuesta en el barrio San José de la ciudad de Medellín para saber el número de estudiantes del nivel preescolar en el 2020, en cada una de las instituciones educativas que existen en dicho sector. Los resultados obtenidos, fueron:
Preescolar Pollitos 45 estudiantes
Preescolar Aprendamos 60 estudiantes
Preescolar Jugando 70 estudiantes
Preescolar San Juan 100 estudiantes
Preescolar La unión 90 estudiantes
Preescolar La Paz 120 estudiantes
De los DATOS que se tienen, podemos decir lo siguiente:
Población Medellín
Muestra Barrio San José
Muestreo Encuesta
Variable Número de estudiantes
Si llevamos la información a una TABLA, tenemos:
De la TABLA anterior, se puede decir:
· La minoría de estudiantes de preescolar son de la institución Pollitos.
· La mayoría de estudiantes, pertenecen al preescolar La Paz.
· El total de estudiantes de preescolar es de 485
· Un alto número de estudiantes de preescolar, pertenecen a la institución de S.J.
La tabla anterior puede ser mucho más general, ya que presentará mayor información.
De la tabla anterior, podemos decir:
· El 9.28 % de los estudiantes, pertenecen al preescolar Pollitos
· El 12.37 % de los estudiantes, pertenecen al preescolar Aprendamos.
· El 14.43 % de los estudiantes, pertenecen al preescolar Jugando.
· El 20.62 % de los estudiantes, pertenecen al preescolar San Juan.
· El 18.56 % de los estudiantes, pertenecen al preescolar La unión.
· El 24.74 % de los estudiantes, pertenecen al preescolar, La Paz.
La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.
Las tablas de frecuencia tienen las siguientes características, una distribución de frecuencias es un formato tabular en la que se organizan los datos en clases, es decir, en grupos de valores que describen una característica de la variable y muestra el número de observaciones del conjunto de datos que caen en cada una de las clases. La tabla de frecuencias ayuda a agrupar cualquier tipo de dato numérico. En principio, en la tabla de frecuencias se detalla cada uno de los valores diferentes en el conjunto de datos junto con el número de veces que aparece, es decir, su frecuencia. Se puede complementar la frecuencia absoluta con la denominada frecuencia relativa, que indica la frecuencia en porcentaje sobre el total de datos. En toda tabla de frecuencias, encontraremos:
La Frecuencia absoluta de una clase, es el número de observaciones que presenta esa clase, es decir el número de veces que se repite la variable. Se representa por las letras fi.
La Frecuencia relativa de una clase, es el cociente entre la frecuencia absoluta fi y el total de observaciones n. Se representa por las letras hi.
La Frecuencia absoluta acumulada, se define como el número de ocurrencias que hay hasta una determinada clase, se representa por las letras Fi. Significa que a cada frecuencia absoluta, se le suma las anteriores.
La Frecuencia relativa acumulada, se define como el cociente entre la frecuencia Fi y el total de observaciones n. Se representa por Hi.
Una tabla de frecuencia, tiene la siguiente forma:
Se hizo una encuesta para saber el número de hijos por familia de un grupo de habitantes del barrio X de la ciudad A en el 2012, los resultados obtenidos fueron:
5, 4, 3, 1, 2, 5, 2, 3, 6, 1, 4, 2, 2, 1, 2, 4, 2, 2, 1, 3.
Ahora se organiza la variable, HIJOS POR FAMILIA en forma ascendente, y se hace el conteo.
De la tabla anterior, podemos concluir que:
·
La mayoría de las
familias del barrio X, solo tienen 2 hijos.
·
La minoría de las
familias del barrio X de la ciudad A, tienen
solo 6 hijos.
·
La moda es tener 2
hijos por familia.
·
El 20% de las
familias tienen 1 solo hijo.
·
El 35% de las
familias tienen 2 hijos
·
el 15% de las
familias del barrio X, tienen 3 hijos.
·
El 15% de las
familias, tienen 4 hijos.
·
Solo el 5% de las
familias del barrio X, tienen 6 hijos
·
El 10% de las
familias, solo tienen 5 hijos.
·
11 familias del
barrio X, tienen entre 1 y 2 hijos.
·
20 familias del
barrio x, tienen entre 1 y 6 hijos.
·
El 85% de las
familias, tienen entre 1 y 4 hijos.
En las tablas
de frecuencia, los DATOS pueden ser AGRUPADOS
y NO AGRUPADOS.
Tablas de frecuencia para datos no agrupados
Los
datos no agrupados son las de observaciones realizadas en un estudio
estadístico que se presentan en su forma
original tal y como fueron recolectados,
para obtener información directamente de ellos. La Tabla de frecuencia de datos
no agrupados indica las frecuencias
con que aparecen los datos estadísticos
sin que se haya hecho ninguna modificación al tamaño de las unidades elementales.
En estas distribuciones cada dato
mantiene su propia identidad después que la distribución de frecuencia se ha elaborado. En estas distribuciones
los valores de cada variable han
sido solamente reagrupados, siguiendo
un orden lógico con sus respectivas frecuencias. Los
datos no agrupados, se identifican ya que su número es inferior a 25 observaciones.
El ejemplo anterior representa
DATOS no agrupados.
jueves, 18 de junio de 2015
Tablas de frecuencia para datos agrupados
Los datos agrupados son aquellos en los que las observaciones estadísticas se
encuentran ordenadas en clases y con la frecuencia de cada
clase; es decir, los datos originales de varios valores adyacentes del conjunto
se combinan para formar un intervalo de
clase. Se identifican porque el
número de observaciones es mayor a 25. Ejemplo
Se hizo una encuesta en la Universidad
de Antioquia sobre un grupo 30 estudiantes del primer semestre
de Medicina, donde se pretende mostrar la edad más representativa.
De
la tabla anterior podemos sacar las
siguientes conclusiones:
·
La mayoría de los estudiantes de medicina tienen edades entre 20 y 22 años.
·
El 20% de los estudiantes tienen entre 23 y 25 años.
·
El 30% de los estudiantes
tienen edades entre 17 y 19 años.
· El 3.3% de los
estudiantes de medicina del 1er semestre tienen edades entre 26 y 28.
· 29 estudiantes de medicina
de la U de A, del 1er semestre tienen edades entre 17
y 31.
·
Solo 21 estudiantes del 1er semestre de medicina, tienen
edades entre 17 y 22 años.
· El 90% de los estudiantes
del 1er semestre de medicina tienen
edades entre 17 y 25 años.
Cuando las variables son CUALITATIVAS, aparecen las modalidades, por lo tanto estas se
deben CODIFICAR para poderlas tabular.
Una variable cualitativa
siempre será cualitativa mientras exprese cualidades (más o menos
subjetivas) de la unidad elemental
observada, pero siempre (o casi siempre) podremos codificarlas para hacerlas manejables y realizar análisis estadísticos con ellas.
Por ejemplo:
La variable, partido político tiene
las siguientes modalidades:
Modalidad Código
Liberal 1
Conservador 2
Uribista 3
Alianza democrática 4
Partido verde 5
La variable Tipo de religión
Modalidad Código
Católico 1
Protestante 2
Evangélico 3
Budista 4
Ortodoxo 5
La variable Estado civil
Modalidad Código
Casado(a) 1
Soltero(a) 2
Separado(a) 3
Unión libre 4
Viudo(a) 5
De la tabla anterior podemos sacar las
siguientes conclusiones:
·
La mayoría de las personas son solteras.
·
La minoría de las personas
están en unión libre.
·
El 20% de las personas del
barrio x, son casadas.
·
17 personas del barrio x,
están casadas, solteras, separadas y en unión libre.
·
El 55% de las personas del
barrio X, están casadas y solteras.
·
La moda en el barrio X, de
la ciudad A es estar soltero.
Suscribirse a:
Comentarios (Atom)