En
estadística denominamos gráficas a
aquellas imágenes que, combinando la utilización de sombreado, colores, puntos, líneas, símbolos, números, texto y un
sistema de referencia, permiten presentar información cuantitativa.
La utilidad de las gráficas es doble, ya que pueden servir
no sólo como sustituto a las tablas, sino que también constituyen por sí mismos
una poderosa herramienta para el análisis
de los datos, siendo en ocasiones el
medio más efectivo no sólo para describir
y resumir la información, sino
también para analizarla.
Una gráfica es la representación de datos, generalmente numéricos, mediante líneas, superficies o símbolos, para ver la relación que esos datos
guardan entre sí. Hay muchos tipos de gráficas estadísticas. Cada una de ellas es adecuada para un
estudio determinado, ya que no siempre se puede utilizar la misma para todos
los casos. Las gráficas más comunes son:
·
Diagrama de barras
·
Gráficos de líneas
·
Histograma
·
Polígono de frecuencias
·
Diagrama de sectores o
gráfica circular.
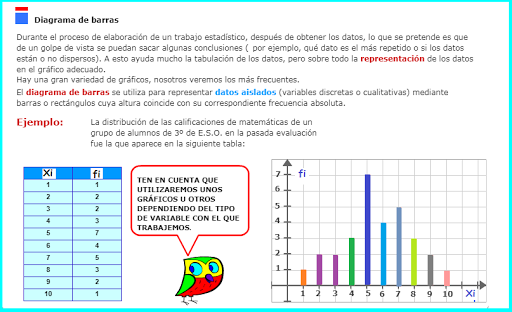
Es
una de las gráficas más utilizadas por su sencillez y por la facilidad que
ofrece para representar las características de las variables. Las barras
que se usan son sencillamente rectángulos
separados entre sí y construidos generalmente en forma vertical.
En
este tipo de gráfica, sobre los
valores de las variables se levantan barras estrechas de longitudes proporcionales a las
correspondientes frecuencias absolutas.
Todas las barras deben ser de igual ancho y estar igualmente espaciadas. Se
utilizan para representar variables cuantitativas
discretas. Por ejemplo
Se puede observar que la gráfica de
barras representa en forma más
global y llamativa toda la información de la tabla estadística.
Las gráficas lineales se utilizan para estudiar la evolución de un fenómeno observado en un cierto tiempo. Además pueden mostrar relaciones visuales y su conexión con otros conceptos matemáticos, son además un medio para registrar información de manera más clara que la registrada en tablas y ecuaciones. Las representaciones gráficas ayudan a asociar la matemática con la vida cotidiana.
Las gráficas de línea son más populares que todos los otros gráficos combinados debido a que sus características visuales revelan tendencias de los datos de manera clara y estos gráficos son fáciles de crear. Las gráficas de línea, especialmente útiles en los campos de la estadística y la ciencia, es una de las herramientas más comunes utilizadas para presentar los datos.
De
la gráfica anterior podemos sacar
las siguientes conclusiones:
· El mayor peso promedio de los alumnos de SEXTO grado, se presentó en el 2010.
·
El menor peso promedio se
presentó en el 2007.
·
La MODA en el peso promedio
para los alumnos de sexto grado del colegio X, de la ciudad A es 70 kg.
·
Se observa que el peso
promedio aumentó 10 kg entre el 2007 y el 2008.
· El mayor aumento del peso
promedio de los alumnos de sexto grado, se presentó entre los años 2009 y 2010.
Podemos notar que las conclusiones son muy importantes en el
análisis estadístico. Estas son más visibles de sacar y observar en las
gráficas.
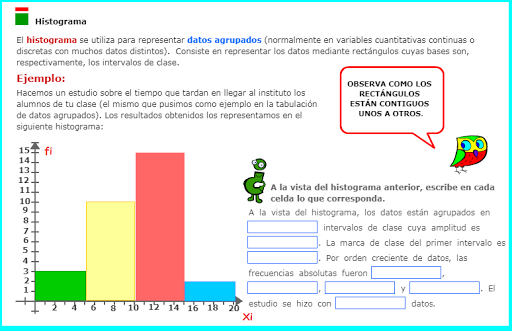
El
histograma es una forma de presentar gráficamente las FRECUENCIAS de los intervalos de clase. Los histogramas se
utilizan para representar tablas de
frecuencias con datos agrupados
en intervalos. Los histogramas y los gráficos de barras se diferencian específicamente
en:
· En
el histograma, la frecuencia no la
determina la ALTURA de los
rectángulos sino el ÁREA de ellos.
· Los
rectángulos se dibujan sin dejar espacios entre ellos.
De
la gráfica anterior podemos sacar
las siguientes conclusiones:
·
La mayoría de los estudiantes de medicina
de la U de A tienen una edad promedio de 21 años.
·
La moda de los estudiantes
de medicina es tener 21 años.
·
La minoría de los
estudiantes de medicina de la U de a, tienen edades promedios entre 27, 30 y 33
años.
·
Solo 9 estudiantes de
medicina, tiene una edad promedio de 18 años.
·
6 estudiantes de medicina,
tienen una edad promedio de 24 años.
Los gráficos circulares,
también llamados gráficos de pastel o gráficas de 360 grados, son
recursos estadísticos que se
utilizan para representar porcentajes y
proporciones. Una manera fácil de identificar los segmentos es sombreando de claro a oscuro, donde el de mayor tamaño
es el más claro y el de menor tamaño, el más oscuro. El gráfico
circular es útil para representar proporciones de distintas clases dentro
de una muestra. La muestra es representada por un círculo y cada una de las clases que la
componen, por un sector de
éste.
La siguiente tabla estadística, nos
muestra el estado civil de un grupo
de personas del barrio X, de la ciudad A.
De la gráfica anterior podemos sacar las
siguientes conclusiones:
·
La mayoría de las personas del barrio X de la ciudad A,
son solteras.
·
La minoría de las personas
están en unión libre.
·
La moda en el barrio x, es
estar soltero.
·
El 20% de los
habitantes del barrio X, son casados.
·
El 15% de los habitantes del
barrio X, son viudos.
Aprovechando todas las herramientas que
nos traen las TIC, y los recursos didácticos en el proceso ENSEÑANZA
APRENDIZAJE de la matemática, en las siguientes direcciones electrónicas
podemos encontrar lecturas complementarias y una serie de animaciones que nos
ayudarán a una mejor comprensión de todo lo relacionando con los sistemas
aleatorios y su aplicabilidad en la naturaleza.
Lógica y conjuntos
Los números naturales
Potencias, radicales y logaritmos en los naturales
Sistemas de numeración
Los números enteros
Teoría de números
Los números fraccionarios
Sistemas geométricos
Estadística












No hay comentarios:
Publicar un comentario